Johannes Kepler a établi trois relations mathématiques, aujourd’hui dites « lois de Kepler » qui décrivent le mouvement des planètes sur leur orbite et permettent d’expliquer le mouvement apparent des planètes dans le ciel.
Kepler ne pouvait pas démontrer ses lois, il lui manquait les lois de la gravitation universelle que Newton établira quelques années plus tard et qui elles, expliquent pourquoi le mouvement s’effectue ainsi et donnent les principes fondamentaux de la mécanique.
Johannes Kepler (1571-1630)
C'est en 1600 que Kepler rejoint l'astronome-observateur Tycho Brahé et devint son assistant. Il se voit alors confier l'étude de l'orbite de Mars qui présentait, depuis l'antiquité, des anomalies dans son mouvement apparent, alors impossible à expliquer. Au début, Kepler pensait résoudre le problème en huit jours! Il lui aura finalement fallu 8 ans pour découvrir la nature elliptique de l'orbite de Mars dans un modèle héliocentrique, et aussi formuler ses deux premières lois qu'il publia en 1609 dans "Astronomie Nouvelle"
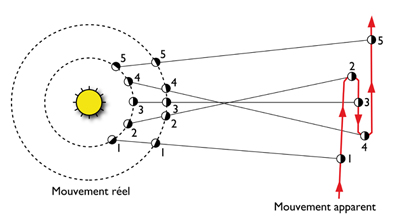
La première loi nous dit qu’au cours de leur mouvement autour du Soleil, les planètes décrivent des ellipses dont l’un des foyers est occupé par le Soleil.
1/ Les coniques
Une conique est une figure géométrique obtenu par l'intersection d'un cône par un plan. Ce plan peut être placé en plusieurs endroits :
- Plan perpendiculaire à l'axe du cône : Cercle
- Plan situé entre la perpendiculaire à l'axe du cône et d'angle d'inclinaison inférieur à l'angle d'ouverture du cône : Ellipse
- Plan d'inclinaison égal à l'angle d'ouverture du cône : Parabole
- Plan d'inclinaison supérieur à l'angle d'ouverture du cône : Hyperbole

Nous avons deux coniques fermées : le cercle et l'ellipse et deux coniques ouvertes : la parabole et l'hyperbole.
Définition de l’ellipse:
L’ellipse est une courbe plane faisant partie de la famille des coniques. Il s’agit d’une courbe plane fermée ayant une excentricité supérieure à 0 et inférieure à 1, obtenue par l’intersection d’un cône de révolution et d’un plan.
En fonction de la valeur de l’excentricité (e), on obtient:
-le cercle (e=0)
-l’ellipse (0<e<1)
-la parabole (e=1)
-l’hyperbole (e>1).
2/ Caractéristiques géométriques :
L'ellipse est le lieu des points dont la somme des distances à deux points fixes, dits foyers, F et F’, est constante.
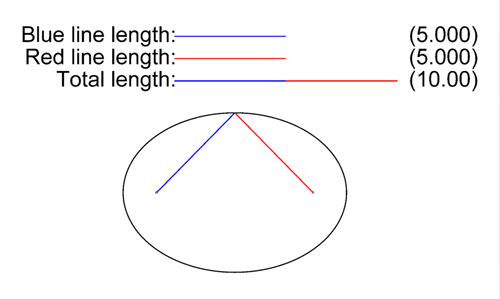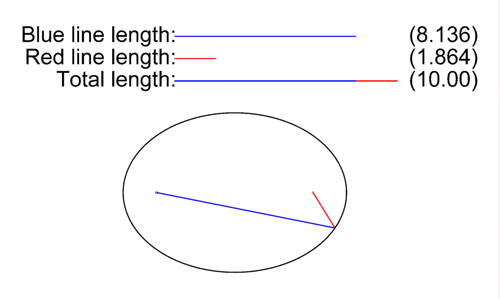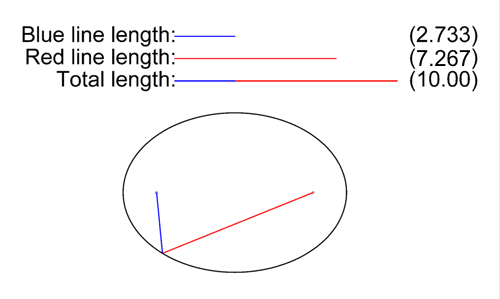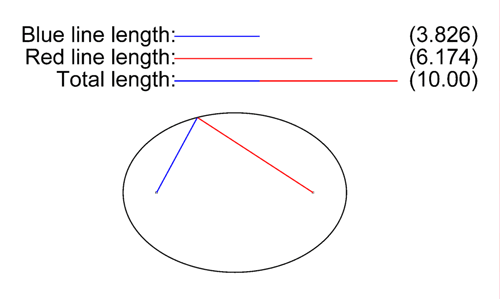
Une ellipse est caractérisée par deux constantes, le paramètre (e), l’excentricité, c'est-à-dire le degré d’aplatissement et le paramètre (p) qui est une constante et défini sa taille sans affecter la forme. On appelle demi grand axe (a) le plus grand de ses demi-diamètres et demi petit axe (b), le plus petit demi-diamètre de l’ellipse.
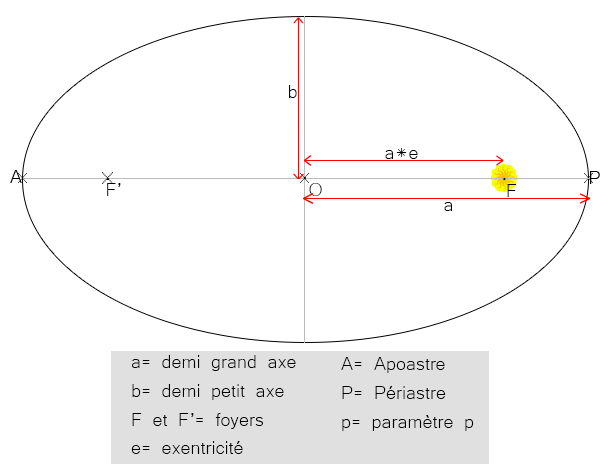
On peut caractériser l’ellipse par les relations suivantes :
3/ En astronomie :
Les deux extrémités du grand axe sont appelées le périastre et l’apoastre. Le périastre étant l’extrémité le plus proche du foyer F et l’apoastre étant l’extrémité le plus loin du foyer F. Pour le système solaire, le soleil étant au foyer F, le périastre se nomme périhélie et l’apoastre, l’aphélie.
Pour le système terrestre si la terre est au foyer F, Le périastre se nomme périgée et l’apoastre, apogée.
La distance maximale du foyer F à l’Apoastre A est FA=a(1+e)
La distance minimale du foyer F au Périastre P est FP=a(1-e)
Sur la ligne de visée, lorsque l’on observe le mouvement d’un astre en orbite autour d’un autre, il y a l’effet de projection, autrement dit l’inclinaison de l’ellipse. Les paramètres de l’ellipse apparents de l’orbite sont différents des paramètres de l’ellipse réelle mais dans la mesure ou le centre de l’ellipse et le foyer est conservé (l’emplacement apparent de l’astre central est le foyer réel F), les rapports sont conservés et on peut donc calculer l’excentricité réelle de l’ellipse. Une fois que l'on a déterminé l'axe de rotation de l'inclinaison et l'angle d'inclinaison, on peut calculer la longueur réelle du demi grand axe.
Tout corps soumis à une force d'attraction proportionnelle à sa masse et inversement proportionnelle au carré de la distance de ce corps avec le corps "central" suit obligatoire une trajectoire en forme de conique. Cette conique est ouverte si la force d'attraction est supérieure à une valeur limite (celle donnant une trajectoire parabolique)
La deuxième loi de Kepler dit qu’au cours du mouvement orbital, le rayon-vecteur joignant les centres du Soleil et d’une planète, balaie des aires égales en des temps égaux. C'est à dire que en une durée donnée, l’aire balayée est toujours la même, quelque soit la partie de l’orbite sur laquelle on se trouve.

L’aire balayée croît à une vitesse constante. Cette vitesse de croissance de l’aire balayée quand la planète se déplace le long de son orbite porte un nom, on l’appelle la vitesse aréolaire, et c’est la dérivée de l’aire balayée par rapport au temps : dA(t)/dt .
Sur une période orbitale complète grand T, la planète est revenue à son point de départ et l’aire balayée est donc l’aire totale de l’ellipse.
Pour une ellipse de demi-grand axe a et d’excentricité e, l’aire de l’ellipse a pour expression:

La vitesse aréolaire peut alors s'obtenir en divisant l'aire balayée par la durée nécessaire pour la balayer, c'est à dire la période t. On obtient donc cette expression plus précise de la deuxième loi de Kepler:
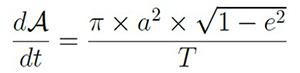
Elle nous permet de relier les paramètres purement géométriques de l’ellipse, comme son demi-grand axe a et son excentricité e, aux paramètres qui décrivent l’évolution temporelle de la planète sur son orbite : la période T et la vitesse aréolaire constante.
La troisième loi de Kepler dit que le carré de la période sidérale notéeT, c'est-à-dire le temps entre deux passages successifs devant une étoile est directement proportionnel au cube du demi grand axe a de la trajectoire elliptique de la planète.

Pour le systeme solaire, on peut considérer la période en année, 1 an pour la Terre, et le demi grand axe en unité astronomique, 1 UA pour la Terre.
Nous avons 1²/1^3=1
Si maintenant nous prenons la planète Mars, nous avons:
1.8808²/1.5237^3=1
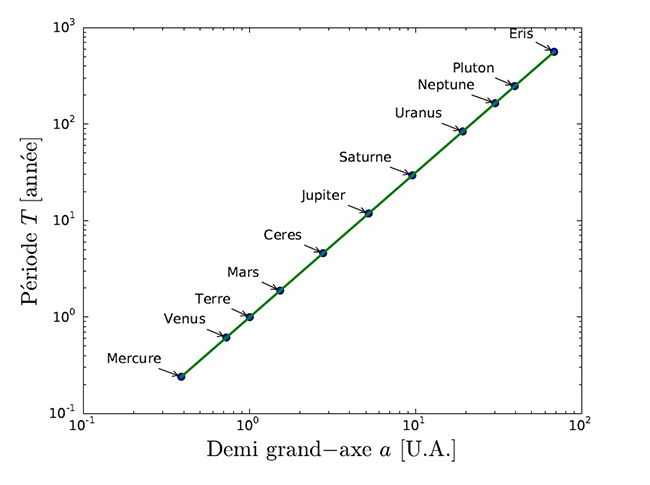
Ce rapport est valable pour tout les objets du systeme solaire orbitant autour du soleil.
Cette constante de proportionnalité entre T carré et a cube, a été déterminée plus tard grâce aux lois de la gravitation universelle établies par Isaac Newton.
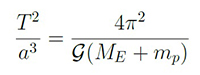
Les lois de la mécanique permettent en effet de montrer que cette constante est fonction de la constante de la gravitation G et de la somme de la Masse du Soleil et de celle de la planète qui gravite autour du Soleil.
Comme en première approximation, la masse de n’importe quelle planète du Système Solaire peut être négligeable devant celle du Soleil, la constante de proportionnalité de la 3° loi de Kepler est le produit de la masse du Soleil est de la constante de la gravitation.
Par exemple, si nous souhaitons calculer la masse du soleil, alors nous avons:
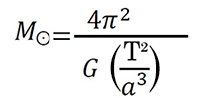
Soit la masse Solaire est égale à: 1,99x10^30Kg, près de 300 000 fois la masse de la terre
La première loi de Kepler décrit la forme de l’orbite de la planète.
la deuxième loi de Kepler décrit complètement le déplacement de la planète sur cette orbite au cours du temps.
La troisième loi de Kepler permet de calculer la masse de l'objet central. Cette troisième loi a joué un rôle particulièrement important dans l’histoire de la physique, puisque c’est à partir de cette loi que Newton a pu construire sa théorie de la gravitation universelle, et, en particulier, déduire que la force de la gravitation doit être inversement proportionnelle au carré de la distance entre les deux corps.
Ci dessous, cette animation flash permet de jouer avec les différents paramètres impliqués dans les 3 lois de Kepler: